当前,各行各业中的隐私泄露问题层出不穷,人们对于隐私安全保护的需求日益提高。随着相关法律法规体系的逐渐成熟,众多隐私计算技术也应运而生,联邦学习就是其中的佼佼者。通过结合同态加密、秘密共享、不经意传输等安全计算方法,联邦学习使得多个数据持有者,可以在保证数据安全的前提下,协同构建机器学习模型。在联邦学习中所使用的多种隐私计算技术中,同态加密的功能和实用性举足轻重。
在各行各业,不难想象这样的场景,A 公司拥有大量数据,然而其并没有人力或计算能力对这些数据进行分析处理,因此,A 公司希望购买 B 公司的计算服务对数据进行处理,但是,A 公司不希望 B 公司获取这些数据的具体信息,因此,如果可以将数据进行加密,再传递给 B 公司进行处理,则可以满足 A 公司的所有需求。因此,在这样的场景下,我们需要一套加密体系,对密文执行的一些运算操作,可以等效为对明文执行的运算。
支持对密文进行运算操作的加密体系,被统称为同态加密,而同态运算则泛指对密文执行的各种运算。根据密文可执行运算的范围,同态加密算法被划分为全同态加密、部分同态加密、近似同态加密等。一般来说,对同态运算没有限制的加密算法被称为全同态加密,而仅支持单一同态运算的加密算法被称为部分同态加密。诚然,全同态加密是一种非常理想、需求巨大的算法,然而,目前主流的全同态加密算法,运算复杂度都相当之高,计算时间之漫长,使其几乎无法在生产行业中实现落地。因此,部分同态加密成为了更加现实的解决方案。Paillier 加密就是一套被广泛使用的部分同态加密算法,它支持密文之间的加法运算。
尽管相对于全同态加密,Paillier 加密的计算效率已经较为可观,但是,相比较于高效的明文处理,Paillier 加密系统还是不可避免地引入了大量计算开销。在大数据相关产业迅速发展的今天,成千上万的数据需要得到实时处理,而传统 CPU 的计算能力已经无法满足需求。
FPGA(Field Programmable Gate Array),全称为现场可编程逻辑门阵列,是一种可以根据需求对底层电路结构进行设计更新的芯片,在通信、图像处理等领域拥有广泛的应用。通过使用 FPGA 内部逻辑资源构建计算电路,例化大量计算引擎,可以提高计算并行度,实现对指定算法的加速计算。传统意义上的 FPGA 开发为 RTL(Register-transfer Level)开发,开发人员通过硬件描述语言(Verilog 或 VHDL)控制寄存器读写、规划时序逻辑等,描述具体的硬件功能。这种开发模式需要大量的开发经验以及较长的硬件开发周期,并不适用于开发人员经验不足或者亟须产出的项目开发。因此,HLS(High Level Synthesis)开发受到了很多开发者,尤其是科研工作者的青睐。HLS 是一种代码综合技术,开发人员可以通过高级语言(C 或 C++)描述运算,HLS 开发套件将高级语言编译为 Verilog 或 VHDL 代码,再生成具体网表。开发者无需关心具体硬件电路的设计,只需构造合理运算逻辑,即可在短期内完成一项 FPGA 工程。
使用 HLS 开发实现基于 FPGA 的 Paillier 加密运算,不仅可以提高计算效率,对于同态加密以及联邦学习的硬件加速探索,也有十分重要的意义。
为了实现硬件加速,合适的算法选择十分必要。基于二进制进行运算的芯片,包括 CPU,都可以轻松实现高效的加法、乘法、位移等运算;然而取模、除法等运算则一直是硬件电路难以啃下的硬骨头,计算效率十分低下,显然 Paillier 加密运算中存在不可避免的取模和幂运算。众所周知,幂运算由若干乘法组成,而模幂运算,可以由大名鼎鼎的快速幂算法拆解为若干少量的模乘运算。
那么是否存在一种算法,无需单独取模,就可以实现模乘运算呢?答案是肯定的,这个算法就是蒙哥马利模乘算法。

图一:蒙哥马利模乘算法。
蒙哥马利算法的基本思想如图一所示,其中 l 为 M 的位宽,k 为基数,一般为 16、32、64 这样远小于 1024,且 FPGA 可以直接进行乘法运算的位宽。可以看到,这个算法本质上是一个二重循环,和普通的大数乘法十分相似,但是该算法通过引入参数 q,保证中间结果可以被整除(被 2 的整数次幂除本质上就是向右移位),从而可以无误差地通过移位操作完成除法,同时保证,完成了移位之后得到的最终结果
一定位于区间[0,2M),从而可以通过一次数值比较和减法,将最终结果限制在[0,M),无形中完成了幂运算。基于蒙哥马利模乘运算,再实现就成为了非常简单的操作,实现的方法也有很多。
系统设计介绍

论文链接:https://arxiv.org/pdf/2007.10560.pdf
来自港科大 iSing Lab 等机构的研究者以蒙哥马利模乘运算为核心,提出了一套基于 FPGA 的同态加密加速体系,如图二所示,该系统被设想为部署在云服务器端,这些服务器属于联邦学习的参与方。该系统包括上位机 CPU 以及 FPGA,二者使用 PCIe 接口通信。CPU 负责机器学习模型的正常训练工作,并将机器学习使用的浮点数编码为适配同态加密方案的大整数,同时它将加密请求分批发送给 FPGA;FPGA 中为 Paillier 加密设计了高性能处理器,且硬件模块被封装为 OpenCL 内核由 CPU 进行调用。接下来,我们对 FPGA 内部高性能处理器的设计进行详细介绍。
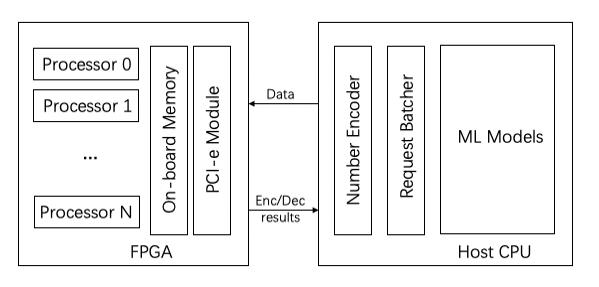
图二:FPGA 联邦学习加速系统。
一个 Paillier 处理器中包含了模幂、随机数生成等所需的运算功能,此 HLS 设计中例化了若干 Paillier 处理器以实现运算的并行处理。此外,为了管理多处理器的工作,需要顶部模块执行数据分发以及计算结果收集的工作。显然,由于 FPGA 内部逻辑资源有限,此系统的运算效率取决于可以例化多少 Paillier 处理器,而 Paillier 处理器的主要组成部分是蒙哥马利模乘。因此,如何在硬件上优化蒙哥马利模乘运算成为了主要工作。我们从资源分配和时序分析两个方面对优化工作进行介绍。
资源分配
对于一个以计算功能为主的 FPGA 工程设计中,DSP、LUT 和 RAM 是总量最有限、最需要仔细规划使用的底层逻辑资源。DSP 是 FPGA 内部实现乘法运算不可缺少的底层逻辑资源,目前主流 FPGA 中的单个 DSP 块,可以在高时钟频率下实现两个 16 比特无符号整数之间的乘法运算,而通过串联多个 DSP 块,可以搭建出位宽更高的乘法器,比如,实现两个 64 比特无符号整数之间的乘法运算需要 16 个 DSP;LUT(lookup table 查找表)是 FPGA 内部最基本的逻辑资源,我们需要结合 LUT 和其他逻辑资源构建加法器、整数比较、有限状态机等其他逻辑电路;RAM 是 FPGA 底层集成的高速存储器,分为 BRAM 和 URAM 两类,一般来说,单个 RAM 可以存储 36Kb 数据,而单个 URAM 可存储 288Kb 数据,在当前工程中,可以使用 RAM 存放输入输出数据以及运算中间结果。
由图一所示,蒙哥马利模乘算法由内外两重循环构成,我们将单次内部循环操作封装为如图三所示的处理单元,每个处理单元中包含两个乘法器,分别用于计算 x*y 和 q*m,两个乘法结果与外层循环的上一轮计算结果以及进位(图中未画出)执行加法操作。同时,为了避免 HLS 编译代码展开循环后,造成乘法器资源大幅膨胀,需要使用 ALLOCATION 指令将处理单元的个数限制为 1 个。
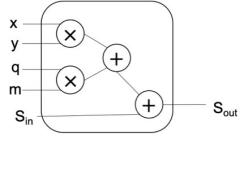
图三:算法 1 内部循环处理单元。

图四:Karatsuba 快速乘法。
在处理单元的设计中,同时采用了 Karatsuba 算法,如图四所示。根据乘法运算的原理,容易看出,乘法运算操作数的位宽减半,则总计算时间将减少至原先的四分之一左右。Karatsuba 算法将整数乘法拆分为了三个位宽仅为原来一半的整数乘法,从而节省了计算时间。根据该算法的原理,可以相应地使用 DSP 资源例化出所需的乘法器。
在 RAM 的使用方面,不难注意到,用于加密的输入数据大多是由浮点数编码而成的,与大整数位宽相比,其有效数字很少。因此,可以将输入数据存储为稀疏向量,即只记录非零元素和它们的索引,减少存储占用。
时序分析
时序分析在 FPGA 开发中的重要性,丝毫不亚于对算法的优化以及逻辑资源的分配。从电路的角度简单来说,如果没有合理的逻辑设计和资源布局,不仅会使得信号传递时间过长,还有可能出现多组信号争抢相同硬件资源,导致局部堵塞的问题。
通常来说,开发者可操控的最小粒度的 FPGA 工作时间为一个时钟周期,而 FPGA 完成一个时钟周期所需的时间由时钟频率决定,即

因此,在降低时钟周期数的同时提高时钟频率,是提升 FPGA 运算性能的有效手段。
一般来说,实现一套算法所需要的时钟周期数由其关键路径所决定,所谓关键路径,就是工作流程中,时间延迟最大的一条路径。通过观察蒙哥马利模乘运算的两重循环,可以整理出,整个运算包含
次乘法,因此,如果我们例化了 n 个乘法器,每个乘法器需要运行 t 个时钟周期,则理想中整个蒙哥马利模乘的时钟周期为。考虑到之前所介绍的内部循环处理单元中的两个乘法可以并行执行,我们可以例化两个乘法器同时进行计算;但是,由于不同的循环之间存在数据依赖关系,因此只能串行执行循环。因此,系统设计的目标是让总时钟周期接近。为了实现这一目标,系统中进行了以下三项优化。
展开内层循环:展开内层循环的最大好处就是将内层循环从一个单一的整体拆解为多个组成部分,从而实现多次迭代中无数据依赖部分之间的时间交叠(overlap),进而最大程度地压缩整体运行时间。该操作可以通过 HLS 中的 UNROLL 指令实现。
将 q 的运算插入内层循环中:蒙哥马利算法中 q 是执行内层循环的前提,但是从 q 的表达式中可以发现,只依赖于 S_i 的部分比特位,因此,当某次迭代中 S_i 的这些比特位计算完毕后,即可同时开始进行下一次迭代 q 中的计算。从而节省这部分的时间开销。
流水线处理外层循环:通过展开内层循环,并且使用 HLS 中的 PIPELINE 指令,设置流水线初始化间隔为内层循环的迭代次数,内层循环将自动地根据拆解的操作执行流水线调度。该流水线处理示意图如图五所示。内层循环展开后被拆分为四个部分 S_0 , S_1 , S_2 和 S_3 。当 S_0 计算完毕后,即可开启下次迭代中 q 的计算。而 q 计算完毕后,下一次迭代计算即可开始。
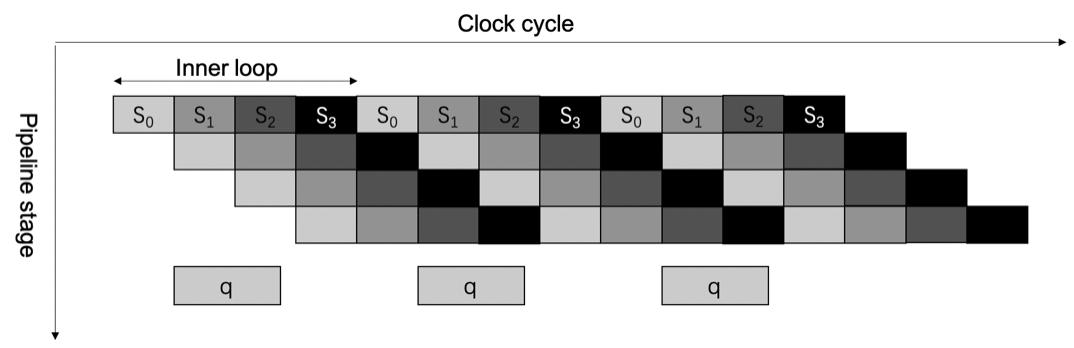
图五:蒙哥马利模乘运算流水线处理示意图。
通过以上处理,不同迭代的运算操作被最大程度地交叠在一起,考虑到完成外层循环所需迭代次数较多,可以近似认为,完成整个蒙哥马利模乘运算所需时钟周期约为。
达成时钟周期的设计目标后,我们还希望能够提高 FPGA 逻辑电路的时钟频率。尽管主流 FPGA 中的 DSP 组件的工作频率都可以达到 400MHz 以上,但是,由于硬件资源的限制,并且考虑到系统中逻辑电路的复杂程度,将整个系统的工作频率提高到这个数值几乎不可能。为了尽力提高工作频率,本系统设计中做出了如下优化:
限制乘法操作数位宽:在蒙哥马利算法的介绍中,我们提及,基数一般选择为 FPGA 可以轻易进行乘法运算的位宽。显然,如果直接将选择为 1024,FPGA 需要漫长的时间才能完成如此大位宽的乘法运算。因此,可以将限制为 32,便于掌控整个时序逻辑。
将乘法器声明为流水(Pipelined)乘法器:流水乘法器可以将大位宽的乘法拆分到多个时钟周期执行,从而缓解紧张的时序。简单来说,如果我们设置系统频率为 200MHz,乘法器几乎不可能在一个时钟周期,也就是 5 纳秒内完成 64 比特整数之间的乘法,但是如果将乘法时间延长到 6 个时钟周期,则乘法器则可以相对容易地在 30 纳秒内完成该乘法操作。
简化控制逻辑:这几乎是 FPGA 开发中不可缺少的优化操作了,通过缩短逻辑电路的长度,可以增加 FPGA 在更高时钟频率下完成信号传递的频率。在本工程中,可以使用独热编码(One-hot Encoding)表示状态机的状态,独热编码可以有效提高状态机的查询和匹配速度,优化时序逻辑。
系统性能测试
完成硬件设计后,通过使用 OpenCL API,上位机可以调用 FPGA 实现运算的硬件加速。我们使用 FPGA 硬件加速内核分别构建了 Paillier 加密和解密运算算子,并对比了它们和 CPU 的运算性能,其中 CPU 的运算通过调用 Paillier 运算库 PHE 实现,对比结果如图六和图七所示。当公钥位宽为 1024 比特时,FPGA 加速系统在加解密运算中分别实现了 10.62 倍和 2.76 倍的加速比。
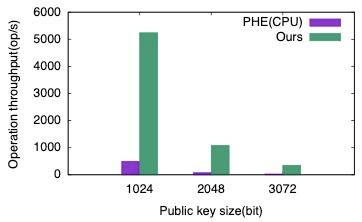
图六:FPGA 和 CPU 加密性能对比。
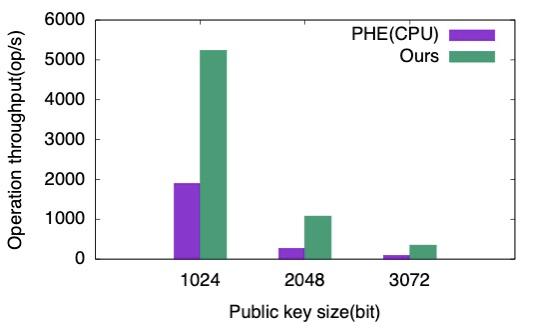
图七:FPGA 和 CPU 解密性能对比。
将 FPGA 硬件加速集成到主流联邦学习框架 FATE 中后,我们也看到了不错的性能提升。我们使用 PyOpenCL API 将 FPGA 硬件加速功能集成为单一模块,嵌入到 FATE 中执行加密运算。分别执行十次逻辑回归迭代和十次线性回归迭代后,我们得到了图八所示的测试结果:FPGA 加速 FATE 削减了原始 FATE 中 71.2% 的加密时间。
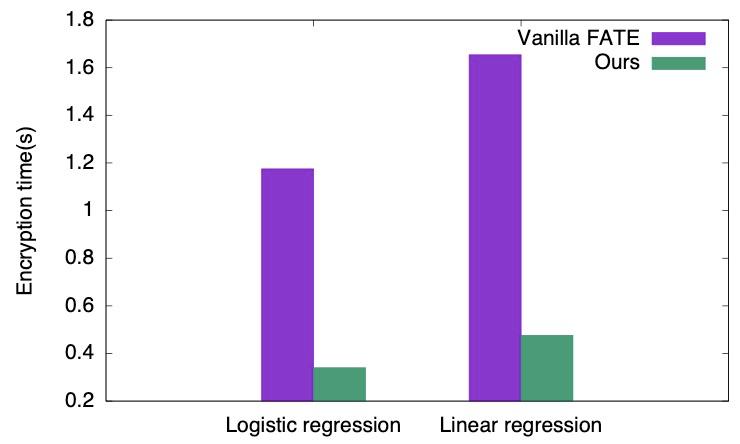
图八:单次训练迭代中 FPGA 加速 FATE 和原始 FATE 的加密时间对比。
总结及展望
同态加密是一种强有力的隐私保护技术,对于它们的探索,是近年来炙手可热的研究方向;FPGA 是一种资源丰富的运算处理芯片,对于高并行度的计算任务可以带来显著的性能提升。对于高性能 FPGA 工程的追求,在当前阶段还是难以摆脱长期的 RTL 开发。通过使用 HLS 快速开发基于 FPGA 的同态加密工程,是对 FPGA 在隐私安全计算行业进行角色定位的有效探索与尝试。近年来,FPGA 的主流供应商 Xilinx 和 Intel 在可编程硬件的高级语言开发上不断增加投入,FPGA 的入手难度也逐渐降低。相信随着数据安全重要性的不断提升,工业界将浮现出更多基于 FPGA 的安全计算产品,而类似于 HLS 的硬件上层开发模式,也将在这个领域逐渐占据一片天地。
本文作者为香港科技大学 iSing Lab 杨照雄、胡水海、陈凯。iSing Lab 是一所专注于高性能数据中心网络、机器学习系统以及联邦学习框架研究的实验室。近 5 年时间中,该实验室在网络系统领域顶级会议 ACM SIGCOMM 和 USENIX NSDI 等定会发布论文 10 篇,根据计算机科学 CSRankings 的排名, 名为亚洲第一。